√画像をダウンロード 円錐 の 体積 の 公式 167512-円錐の体積の公式証明

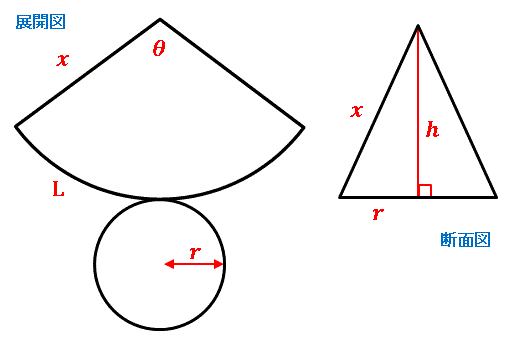
数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。 公式 V=1/3hπr2を、中学生にもわかるように、導き方を教えていただきたいのです。 特に、1/3をかけるところが、納得いかないのです。 (1/2じゃないのはなぜ?)こんな模型は?円錐は難しいから、まず、角錐から。立方
円錐の体積の公式証明
円錐の体積の公式証明- シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体積への拡張 一応最初なので、シンプソンの公式を復習しておきましょう。体と錐体の体積が 常に一定の関係に あることを理解す る。 ④錐体の体積を式 に表現する ⑤角錐や円錐の 辺,半径,高さな どを決めて体積を 求める。 これまで学習してき たことから, 同じ底面積で同じ高 さを持つ錐体と柱体 の関係は, (錐体の体積)
積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
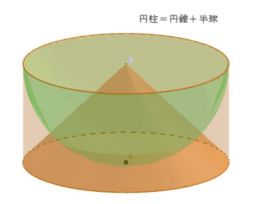
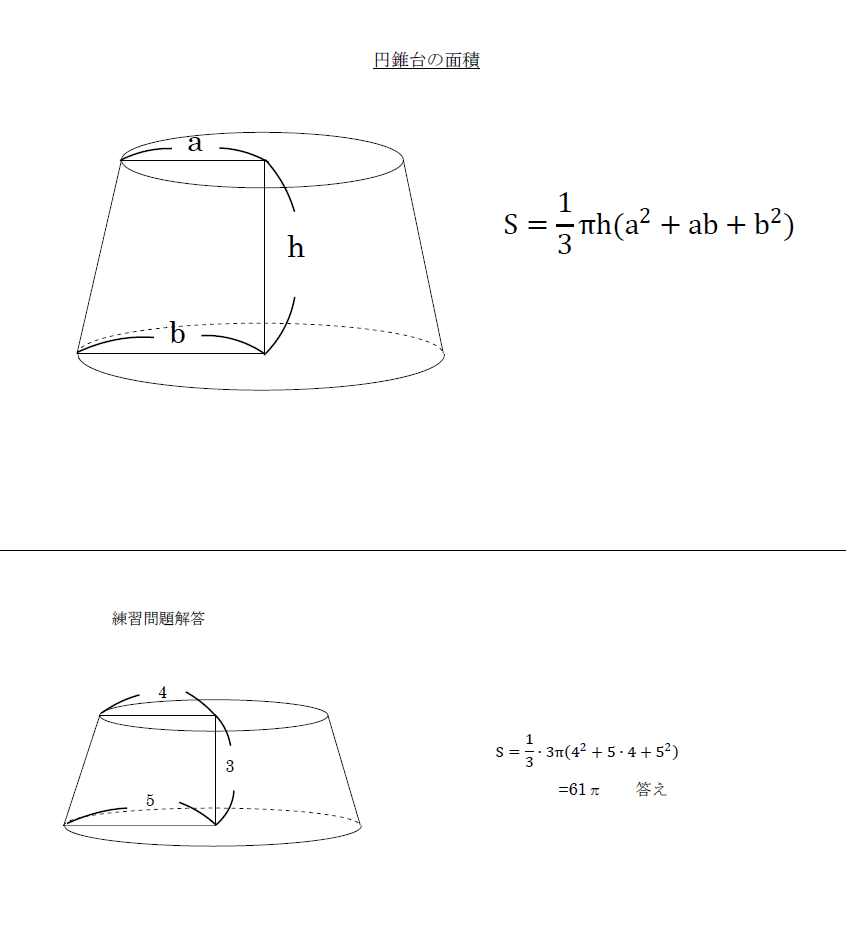
またまた「小中学生にもわかる」シリーズだが、 今回は「錐体の体積は底面積×高さ÷3」 という公式についてである。 この公式は小学校高学年で教わることになっているが、 子供に 「なんで÷3かわかる?」 と聞くと、円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S錐体の体積の場合は、b=0で、c=a/4 (2乗に比例する)だから、 そうすると、4次元錐体の体積は、b=0で、c=a/8 (3乗に比例する)だから、 となるはず。 s:へー。あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。
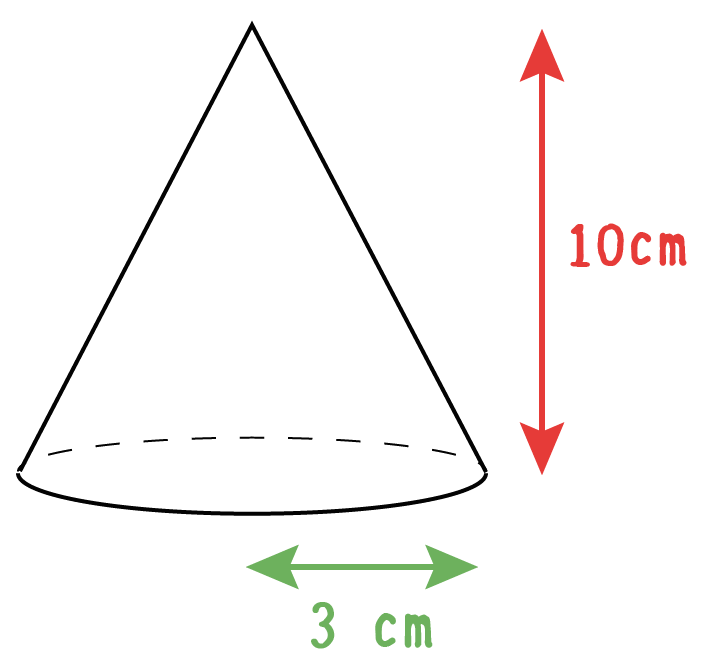
体積はどちらも 『体積=底面積×高さ×\(\dfrac{1}{3}\)』 となります。 このときの "高さ" とは、 頂点から底面に下ろした垂線の長さ です。 角柱や円柱の場合体積は「底面積×高さ」でしたが、錐体の場合これに\(\dfrac{1}{3}\)をかけます。 公式の覚え方 中学校では次のような公式を習うかと思います。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べてい 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱
円錐の体積の公式証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円錐の体積の公式証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
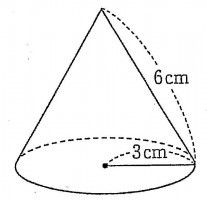
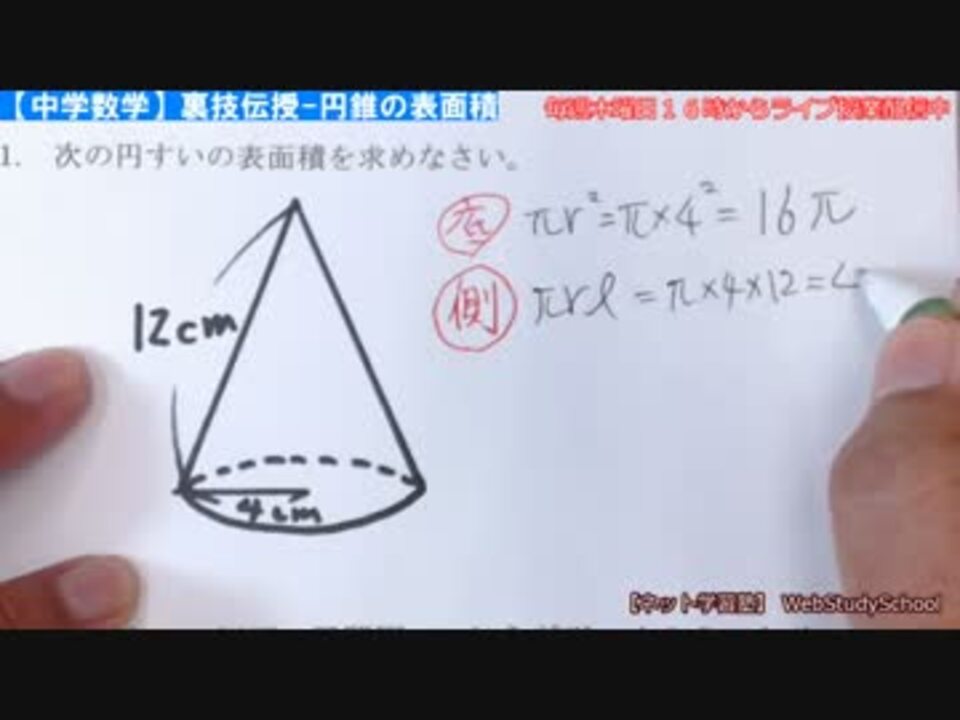
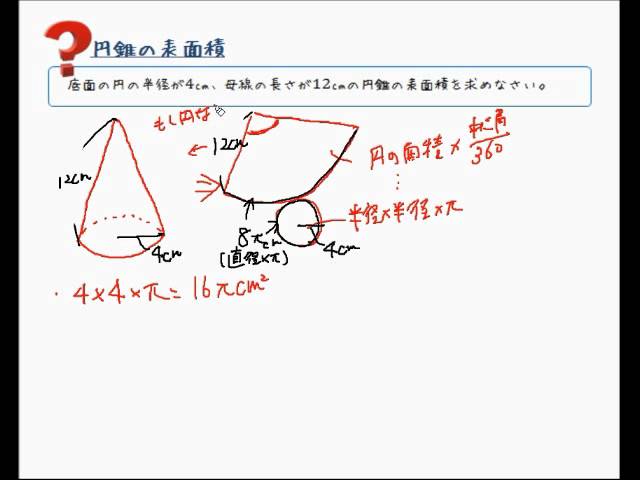
円錐の表面積を求める公式は、S = πr(rR) で表されます ♦ このページでは、「公式を使う場合」と「使わない場合」に分け、円錐の表面積の求め方を例題と共に説明しています。円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより
Incoming Term: 円錐の体積の公式, 円錐の体積の公式証明,
コメント
コメントを投稿